Today, let’s spare a little time to talk about Big O Notation! 😉 As programmers, we often find ourselves asking the same two questions over and over again:
- How much time does this algorithm need to complete?
- How much space does this algorithm need for computing?
To put it in other words, in computer programming, there are often multiple ways to solve a problem, so
- How do we know which solution is the right one?
- How do we compare one algorithm against another?
The big picture is that we are trying to compare how quickly the runtime of algorithms grows with respect to the size of their input. We think of the runtime of an algorithm as a function of the size of the input, where the output is how much work is required to run the algorithm.
To answer those questions, we come up with a concept called Big O notation.
- Big O describes how the time is taken, or memory is used, by a program scales with the amount of data it has to work on
- Big O notation gives us an upper bound of the complexity in the worst case, helping us to quantify performance as the input size becomes arbitrarily large
- In short, Big O notation helps us to measure the scalability of our code
Time and Space Complexity
Big O notation is an important idea that is used in software and web development. It gives an indication of the efficiency of an algorithm, or more specifically, the time and space taken by it.
Time complexity on the other hand is the computational complexity that defines the amount of time that an algorithm takes to run in relation to the size of the input to the program. We consider an algorithm better if it takes less time to complete; the time complexity of an algorithm directly influences this duration.
While space complexity refers to the amount of memory an algorithm requires, or the space it occupies. An algorithm that takes up less memory space is regarded as better than the one that occupies more space.
One of the recent reports pointed out that the use of efficient algorithms can bring down the time complexity from n² to n log n. This means that an algorithm that used 10 hours to sort 10 million items can now use less than 20 minutes.

Likewise, space efficient algorithms are gradually gaining the significance in the field of web development. For example, an algorithm with space complexity of O(n) will need 1 GB of space to process 1 million items. But if we can bring down the space complexity to O(1), the same algorithm would require less than 5MB of space only.
Let’s imagine a web application designed to process thousands of requests per second. If we don’t optimize the algorithms that the application relies on, it could slow down or even freeze. However, with big O notation, developers are able to select the best algorithms for the applications.
Best case — being represented as Big Omega – Ω(n)
Big Omega notation represents the best case scenario in algorithm analysis. We denote this notation as Ω(n), which sets the lower bound of time complexity. It assures us that no matter how sorted the data is, the execution time of an algorithm will not be better than the specified time complexity.
So let’s think about a realistic scenario connected with web development. Suppose you have been given a sorted list and you have to search for a particular element in it. The first case is the best case scenario which is when the desired element is the first element in the list. In this case, the search operation will take Ω(1) time which implies that it will take constant time to perform the operation.
However, not all algorithms have such an optimistic best case, as it depends on the problem that the algorithm is solving. For instance, software developers use the Bubble Sort algorithm, which has a best case time complexity of Ω(n^2). Even when the list is already sorted, Bubble Sort still makes n^2 comparisons for a list with n elements.
It is important for developers to know the best case time complexity. It assists them to select the most suitable algorithm for their purpose, thus improving the functionality of their applications.
Just to recap, Big O notation is only part of the picture. To understand the efficiency of an algorithm one must consider the worst case or Big O, the best case or Big Omega and the average case or Theta. Altogether, these notations give a full picture of an algorithm’s performance.
Average case — being represented as Big Theta – Θ(n)
When it comes to Big O notation, one must be aware of the average case scenario. This is depicted as Big Theta – Θ(n). Now let’s look at what this means in the world of software and web development.
Big Theta – Θ(n) is the average time complexity of an algorithm. It is the average of the best case which is the minimum time and the worst case which is the maximum time. For example, let us take a function that performs a search of an item in an unsorted list. In the worst case, the function might have to search through half of the list to locate the item. This scenario is represented as Θ(n/2), which in Big O notation simplifies to Θ(n) since we always discard constants.
The latest researches in the field of algorithm analysis reveal a trend towards the consideration of average case time complexity. Programmers are beginning to recognize that knowing the mean of their algorithms’ performance can increase the effectiveness and dependability of the software.
Now let us take an example from the real world. Assume that you are working on a web application that often requires the use of a sorting algorithm. If your algorithm is of average time complexity of Θ(n log n) like the Merge Sort algorithm, then it is efficient as the size of the data increases. It is hoped that this understanding of Big O notation and time complexity will aid you in your decision-making process when it comes to writing code which in turn will lead to improved software and web applications.
Worst case — being represented as Big O Notation – O(n)
When talking about Big O Notation, one must always keep in mind what is considered the worst-case scenario, which is O(n). This notation means that the time required to solve a problem increases in direct proportion with the size of the input data set.
Consider a simple task in web development: looking for a specific value in an array that is not sorted. The worst case arises when the value is at the last index of the array or is not in the array at all. In this case the algorithm has to go through the entire array which gives a time complexity of O(n).
Recent research has revealed that the comprehension of Big O Notation in software development can enhance the efficiency of code by a large extent. It assists the developers in choosing which algorithms to employ while working with huge data sets.
For instance, let us take a case of social media app such as Facebook. In the case of a friend search, the application could take a very short time to go through millions of records. An algorithm with a worst-case time complexity of O(n) would therefore be slower with a large number of users. Hence, it is essential to comprehend and take into account Big O Notation in such cases.
Programmers typically solve for the worst-case scenario, Big O
As for Designveloper, we are all about solving the problem. Big O notation is one of the most important tools we employ in our software and web development projects. This mathematical concept assists in determining the rate at which an algorithm will run as the size of the input increases.
This is especially the case when we are creating software, because one always has to think of the worst-case scenario. This is where Big O notation comes into play. It indicates the worst-case scenario of an algorithm’s time complexity. In other words, it provides an upper bound on the time complexity of an algorithm in relation to the size of the input.
For instance, let us describe one of our projects, Lumin. Lumin is an application that is used in the management of documents, particularly PDF documents with features such as viewing, editing, and sharing. When designing Lumin, it was also important to know how the application would act as the number of users and documents grew. Thus, the usage of Big O notation allowed for the prediction of the application’s performance and its scalability.
Another example is the work that has been done on Bonux which is a crypto wallet that investors can use for storage, management and performing transactions within the wallet. Given that there could be thousands of transactions taking place in a second, the time complexity of our algorithms was important. Big O notation helped us to guarantee that our algorithms were capable of handling this load.
Our company has been working for 11 years, and during this time we have completed over one hundred projects, using over fifty technologies in more than twenty industries. In many of these projects, we have employed Big O notation to guarantee that our solutions are efficient and scalable.
How to Calculate the Big O of an Algorithm?
Suppose we want to write a function that calculates the sum of all numbers from 1 up to (and including) some number.
Question: How do we know which one is better? Can we use the time to measure it?
Answer: The problem with time is that different machines will record different times. The same machine will sometimes record different times. For fast algorithms, speed measurements may not be precise enough.
Question: If not time, then what?
Answer: Rather than counting seconds, which are so variable. Let’s count the number of simple operations the computer has to perform.
This function will take 3 simple operations, regardless of the size of n. If we compare the below function, we have a loop and it depends on the value of n.
We can see that as n grows towards some large number approaching infinity, the number of operations that we have to do will also grow at least in proportion to n.
4 rules to find the Big O complexity of an algorithm
At Designveloper, we’ve delivered over 100 projects across 20+ industries, applying over 50 technologies. Our experience in software development has given us a deep understanding of Big O notation, a crucial concept in computer science. Here are four rules to find the Big O complexity of an algorithm:
- Identify Basic Operations: The simplest level of an algorithm is the basic operations. For example arithmetic operations, comparisons and assignments. The first thing that should be done is to distinguish these operations as they are directly related to the time complexity.
- Count the Operations: Next, count the number of basic operations. This count will depend on the size of the input, that is the number of words in the input. For example, in linear search algorithm, the number of comparisons is equal to the number of elements in the list.
- Find the Worst-Case Scenario: That means, Big O notation describes the upper bound of the time complexity of an algorithm. Thus, find out the maximum number of operations that could be performed on any input of size n.
- Simplify: Last of all, write the number of operations as the order of growth, which gives a simple indication of the worst case scenario. For instance, if the number of operations is 3n^2 + 2n + 1 the Big O notation will be O(n^2) since we only consider the highest degree of n.
Big O notation is crucial for designing good software and web applications. It enables developers to decide which algorithms to use. This in turn results in better performance and improved user experience. At Designveloper, we always follow these principles in all of our projects so that we can provide the best services.
Big O Complexity Chart
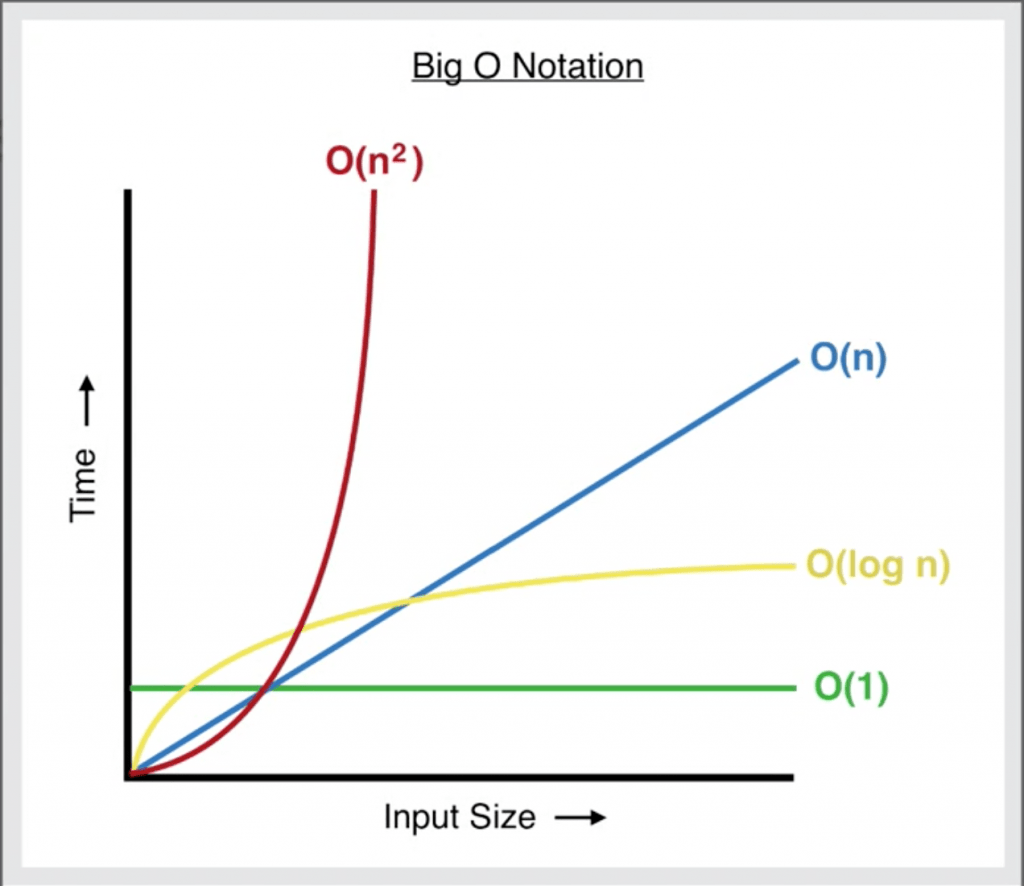
When talking about scalability, programmers worry about large inputs (what does the end of the chart look like). When writing code, we tend to think in here and now. For example, we think that our website or our app will only have a few hundred users and that’s it. If we know our input is going to be small (ex: an array of 5 items), Big O won’t matter as much. But what if that user base grows, what if our inputs grow? We never know that.
In real-life scenarios, we want to write code that can scale, so we don’t have to go back and fix things or when it gets out of hand, the code won’t break. The Big O chart helps us to think about our code/algorithms in the long term and think about what could happen in the future.
Cheatsheets
- O(1) Constant- no loops
- O(log N) Logarithmic- normally searching algorithms have log n if the input is sorted (Binary Search)
- O(n) Linear- for loops, while loops through n items
- O(n log(n)) Log-Linear – usually sorting operations
- O(n^2) Quadratic- every element in a collection needs to be compared to every other element. Two nested loops
- O(2^n) Exponential- recursive algorithms that solve a problem of size N
- O(n!) Factorial- we are adding a loop for every element
- Iterating through half a collection is still O(n)
- Two separate collections: O(a * b)
That’s all. People from Designveloper hope that this article has provided some useful information about Big O Notation for you! Cheers!
For more articles like this, just follow our SNSs (Facebook, Twitter, LinkedIn) now!





Read more topics