Today, there’s a wide range of data structures out there to store and organize data elements. Linear data structures like arrays or linked lists are fundamental in computer science, yet they present some limitations, especially in time complexity for many operations.
In other words, such operations as finding or inserting data elements often require moving through the entire linear data structure. When the amount of data increases, these operations become extremely time-consuming. This is unacceptable for many applications like big data analytics, machine learning, or systems (e.g., online gaming servers) that need instant responses.
To solve this problem, we need to count on non-linear data structures, like trees or graphs. It’s because they provide more effective operations, especially on vast data volumes.
With the booming of the Internet and social media platforms, the amount of data we create, store, and consume everyday has become increasingly large, with 181 zettabytes estimated in 2025. Therefore, we’ll witness a wider adoption of non-linear data structures in the future. Here in this article, we’ll focus on one common data structure in this group – that’s Tree. So, what’s it, and how does it work? Let’s find it out!
Overview of Tree Data Structures
In the first section, we’ll give you a quick, yet detailed overview of a tree data structure by answering the following questions:
Recommended reading: What Is Data Structure and Their Applications?
Q: What is a Tree data structure?
A tree is one data structure that helps represent hierarchical data. For example, let’s say you want to show employees in an organization and their positions in an organizational hierarchy. Here’s how you show it like this:
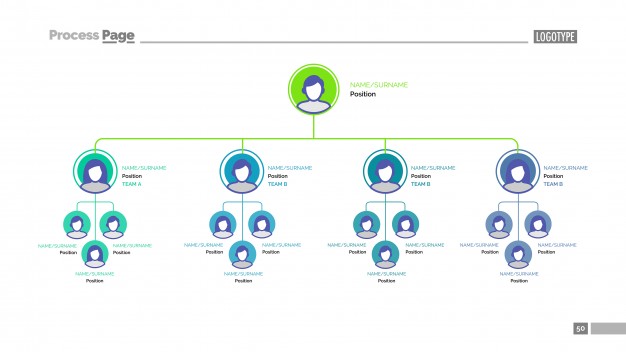
This particular logical structure in the image above is a Tree. If you look at this structure upside down and then it will resemble a real tree. The root here is at the top and you are branching out in a downward direction. The logical representation of the tree data structure is always like that. Root at the top and branch out in a downward direction.
Q: What components does a Tree include?
A tree data structure is a collection of entities called nodes linked together to simulate a hierarchy. The topmost node in the tree is called the root of the tree. Furthermore, each node will contain some data and this can be data of any type. In other words, each node will contain some data and may contain a link or reference to some other nodes that can be called its children.
In the image above, data is the name of the employee and their designation. Accordingly, you may have an object with two string fields to store that info.
Q: How does a Tree work?
A tree works in accordance with the following basic operations:
- Create: The first step is to create a new tree.
- Insert: Next, you’ll add new data elements to the tree.
- Search: Then, you’ll search for a particular piece of data in the tree to check whether it exists.
- Traversal: The final step is to traverse each data element in the tree in a special order. There are two primary ways that help you do this. First, you can use the Depth-First Search (DFS) method that traverses as deep as possibly along one branch before going to another. Meanwhile, the other approach, known as Breadth-First Search (BFS), moves through each level to visit all data elements before traversing to the next.
Q: When can you use a Tree?
With what we described above, you may seemingly envision when to use a Tree. Here are several applications of a Tree data structure in real life:
1. Hierarchical Structure
A Tree is an efficient way of storing and organizing data that is naturally hierarchical – or in other words, has layers. One typical example is a folder containing other folders and files to form a tree structure on a computer.
Similarly, the Domain Name System (DNS) also has a tree structure that organizes domain names in layers, with the broadest categories (“top-level domains”) like .com or .org serving as the “root” layer of the hierarchy. Each top-level domain, accordingly, will have second-level domains (which are often the names of websites like “designveloper” in designveloper.com).
2. Efficient Search
Trees speed up searches. For example, in a binary search tree, looking for a data element is much faster than sifting through a linear data structure as you don’t need to check every element one by one. Instead, you can go directly to parts of the tree that contain that element. This is especially useful when you have to deal with massive datasets.
3. Efficient Organization
Trees assist in sorting data in a consistent, orderly way. For example, data elements are often automatically organized in a self-balancing binary search tree after they’re added. This allows you to look for the largest, smallest, and other specific values faster.
4. Dynamic Data
Trees can grow or shrink when you add or remove nodes. Therefore, they’re helpful in processing data that regularly changes, particularly in real-time applications such as chat apps, gaming apps, navigation & GPS systems, or stock trading platforms.
FURTHER READING: |
1. What Is Big O Notation? |
2. Stacks and Queues in Data Structures: An Overview in 2022 |
Types of Tree Data Structures
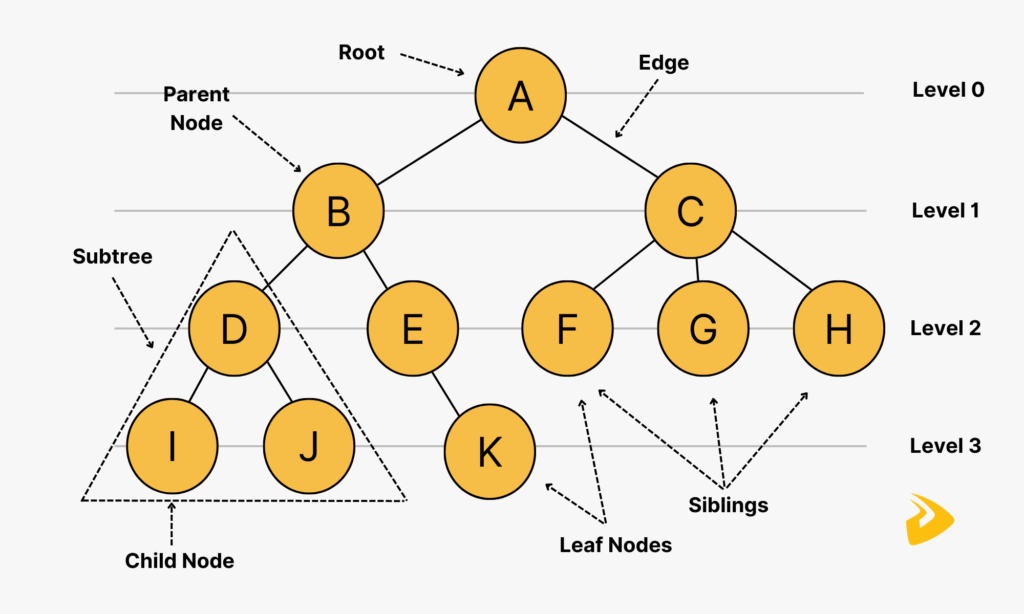
Various types of trees have been created throughout the past years, to suit certain apps and meet certain constraints or requirements. Some examples are binary search tree, B tree, red-black tree, splay tree, treap, AVL tree, and n-ary tree. Let’s take a closer look at some of them.
Binary Search Trees
A binary search tree (BST), as the name indicates, is a binary tree where data is organized in a hierarchical structure. This data structure stores values in sorted order. A BinaryBinary Tree is a Tree in which each node can have at most 2 children.
Every node in a binary search tree comprises four attributes.
- key: The value stored in the node.
- left: The pointer to the child on the left
- right: The pointer to the child on the right.
- p: The pointer to the parent node.
A binary search tree has a unique property that distinguishes it from other trees. This property is known as the binary-search-tree property.
Let’s assume that A is a node in a binary search tree.
- If B is a node in the left subtree of A, then B.key ≤ A.key
- If B is a node in the right subtree of A, then B.key ≥ A.key
Application of a Tree in Computer science
- Storing naturally hierarchical data. For example, the files system in our computer disk driver is stored in the form of a Tree. The file and folder hierarchy is naturally hierarchical data.
- Organizing data for quick search, insertion, and deletion. Example: Binary search trees can give us O(log n) time for searching an element in it. This is so fast and effective when we want to look for a specific element.
- Trie: is a special kind of Tree used to store dictionaries. It’s really fast and efficient and is used for dynamic spell checking
- Network Routing algorithm
Heaps
A Heap is a special case of a binary tree where the parent nodes are compared to their children with their values and are arranged accordingly.
Let us see how we can represent heaps. Heaps can also be represented using trees as well as arrays. The following images show us how we can represent a binary heap using a binary tree and an array.
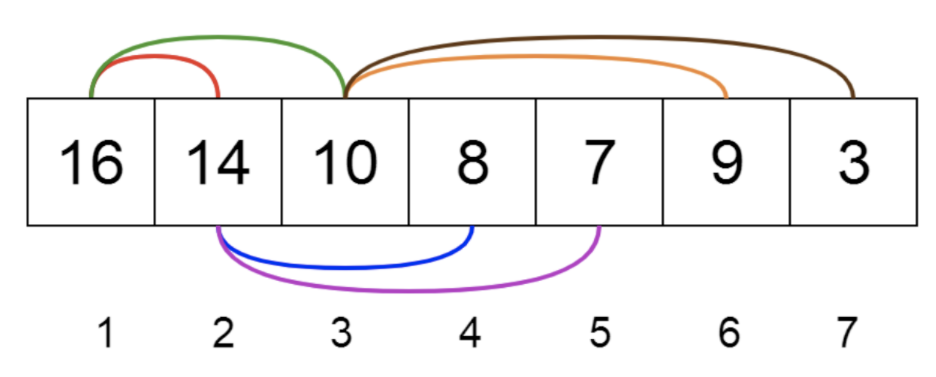
Heaps can be one of two types:
- Min Heap — the key of the parent is smaller than or equal to those of its children. This is known as the min-heap property. The root will contain the heap’s minimum value.
- Max Heap — the key of the parent is bigger than or equal to those of its children. This is known as the max-heap property. The root will contain the heap’s maximum value.
Applications of Heaps
- Used in a heapsort algorithm.
- Helpful in implementing priority queues as the priority values can be ordered according to the heap property where the heap can be implemented using an array.
- Queue functions can be developed using heaps with O(log n) time complexity.
- Used to find the kᵗʰ smallest (or biggest) value in a given array.
How to Choose the Right Data Structure
Our choice of data structure depends upon several factors:
- What needs to be stored? A certain data structure can be the best fit for a particular kind of data.
- Cost of operations. Quite often, we want to minimize the cost of the most frequently performed operations.
- Memory consumption. Sometimes, we may want to minimize the memory usage.
- Easy implementation. We may also choose a data structure for ease of implementation, although this may not be the best strategy.
Conclusion
This article gave you a detailed look at what a tree data structure is and how it works to benefit computer science. Choosing the right data structure will help you manage data and implement different programming tasks effectively. For more articles like this, just follow our Facebook, LinkedIn, and Twitter or subscribe to our blog!





Read more topics